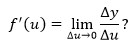Penerapan Kesebangunan

         Bangun-bangun datar yang sebangun ialah bangun-bangun datar yang mempunyai bentuk yang sama namun ukurannya berbeda.

Syarat kesebangunan ialah:

1.     Panjang sisi-sisi bersesuaian pada bangun-bangun tersebut memiliki perbandingan yang sama.

2.     Sudut-sudut yang bersesuaian pada bangun-bangun tersebut sama besar.

Contoh penerapan kesebangunan dalam kehidupan sehari-hari

         Seorang murid ingin mengganti tali yang ada pada tiang bendera di sekolahnya. Oleh karena itu, ia perlu mengetahui berapa tinggi tiang bendera. Untuk keperluan tersebut, ia berdiri di dekat tiang bendera pada pagi hari dan diketahui panjang banyangan murid tersebut 3 m. Sedangkan panjang bayangan tiang 8 m. Jika tinggi murid tersebut 1,5 m, maka berapakah tinggi tiang bendera?

Penyelesaian

Dari soal tersebut dapat di buat sketsa sebagai beriikut

Kemudian untuk memperjelas sketsa tersebut maka dibuat gambar kesebangunan

         Karena $\Delta \mathrm{ABC}$ dan $\Delta \mathrm{ADE}$ sebangun, maka perbandingan antara sisi yang bersesuaian sama.

Dengan demikian

$\frac{\mathrm{BC}}{\mathrm{DE}}=\frac{\mathrm{AB}}{\mathrm{AD}}$

$\iff \frac{1,5}{\mathrm{DE}}=\frac{3}{8}$

$\iff \mathrm{DE}=\frac{1,5\times 8}{3}$

$\iff \mathrm{DE}=\frac{12}{3}$

$\iff \mathrm{DE}=4$

         Jadi, tinggi tiang bendera adalah 4 m.

Tugas media dengan menggunkan geogebra

Luas Permukaan Kerucut

         Kerucut merupakan bangun ruang sisi lengkung yang menyerupai limas segi-n beraturan yang bidang alasnya berbentuk lingkaran.

         Luas permukaan kerucut dapat dihitung dengan menambahkan luas alas kerucut yang berbentuk lingkaran dengan luas selimut kerucut. selimut kerucut merupakan sisi permukaan tegak yang melengkung.

         Berdasarkan "Gambar 2. Jaring-jaring kerucut" luas selimut kerucut dapat ditentukan sebaggai berikut:
$\frac{{\mathrm{Luas\; juring\; TABA}}^{\prime }}{\mathrm{Luas\; lingkaran\; berpusat\; di\; T}}=\frac{{\mathrm{Panjang\; busur\; ABA}}^{\prime }}{\mathrm{Keliling\; lingkaran\; berpusat\; di\; T}}$
$\iff \frac{{\mathrm{Luas\; juring\; TABA}}^{\prime }}{ℼs^2}=\frac{2ℼr}{2ℼs}$
$\iff {\mathrm{Luas\; juring\; TABA}}^{\prime }=\frac{r}{s}\times ℼr^2=ℼ\mathrm{rs}$
Karena luas juring TABA' adalah luas selimut kerucut. Jadi, luas selimut kerucut dapat dirumuskan:
                                  $L_s=ℼ\mathrm{rs}$
dimana:
$L_s=\mathrm{Luas\; selimut\; kerucut}$                 $r=\mathrm{jari-jari\; alas\; kerucut}$
$s=\mathrm{garis\; pelukis\; kerucut}$                 $ℼ=\frac{22}{7}$  atau  $ℼ=3,14$
Sedangkan, luas permukaan kerucut (L) dinyatakan sebagai berikut:
$L=\mathrm{Luas\; selimut\; kerucut}+\mathrm{Luas\; alas\; kerucut}$
$L=ℼ\mathrm{rs}+ℼr^2$
$L=ℼr\left(s+r\right)$
Jadi, rumus luas permukaan kerucut dapat dinyatakan sebagai berikut:
                                  $L=ℼr\left(s+r\right)$

Tugas Media Menggunakan Gambar

6. Turunan Fungsi

         Diketahui dengan dan Jika fungsi dapat diturunkan di x = a, untuk a bilangan real maka

Oleh karena a bilangan real maka

Dengan cara yang sama, dapatkan Anda memperoleh

Untuk mendekati nol maka mendekati nol sehingga

, sehingga . Untuk maka .

Contoh 8.15

Tentukan turunan fungsi berikut ini
a.                               c.     .
b.    
Jawab
a.   
Misalkan,maka sehingga
        
b.   
        
c.   
              

Tugas Media dengan menggunakan MathML

6. Turunan Fungsi $y=u^n$

         Diketahui $y=f\left(u\right)$ dengan $f\left(u\right)=u^n$ dan $u=g\left(x\right)$. Jika fungsi $u=g\left(x\right)$ dapat diturunkan di $x=a$,
untuk $a$ bilangan real maka
$g^{\prime }\left(a\right)=\underset{\Delta x\to 0}{\lim }\frac{g\left(a+\Delta x\right)-g\left(x\right)}{\Delta x}$
         Oleh karena $a$ bilangan real sebarang maka
         $g^{\prime }\left(x\right)=\underset{\Delta \times \to 0}{\lim }\frac{g\left(a+\Delta x\right)-g\left(x\right)}{\Delta x}\to g^{\prime }\left(x\right)=\underset{\Delta x\to 0}{\lim }\frac{\Delta u}{\Delta x}$
         Dengan cara yang sama, Dapatkah Anda memperoleh
$f^{\prime }\left(u\right)=\underset{\Delta u\to 0}{\lim }\frac{\Delta y}{\Delta u}$?
         Untuk $\Delta x$ mendekati nol maka $\Delta u$ mendekati nol sehingga
$f^{\prime }\left(u\right)=\underset{\Delta x\to 0}{\lim }=\frac{\Delta y}{\Delta u}\mathrm{dan}{g}^{\prime }\left(x\right)=\underset{\Delta u\to 0}{\lim }\frac{\Delta u}{\Delta x}$
$\underset{\Delta u\to 0}{\lim }\frac{\Delta y}{\Delta u}\underset{\Delta x\to 0}{\lim }\frac{\Delta u}{\Delta x}=f^{\prime }\left(u\right)g^{\prime }\left(x\right)$
$\iff \underset{\Delta u\to 0}{\lim }\frac{\Delta y}{\Delta u}\frac{\Delta u}{\Delta x}=f^{\prime }\left(u\right)g^{\prime }\left(x\right)$
$\iff \underset{\Delta u\to 0}{\lim }\frac{\Delta y}{\Delta x}=f^{\prime }\left(u\right)g^{\prime }\left(x\right)$
$\iff y^{\prime }\left(x\right)=f^{\prime }\left(u\right)g^{\prime }\left(x\right)$
$f\left(u\right)=u^n$, $f^{\prime }\left(u\right)=n{u}^{n-1}$ sehingga $y^{\prime }\left(x\right)=n{u}^{n-1}{u}^{\prime }\left(x\right)$.
Untuk $y=u^n$ maka $y^{\prime }$ = n u⁡ n - 1 u⁡ ′ x .

Contoh 8.15

Tentukan turunan fungsi berikut ini
a.    $f\left(x\right)={\left(2+3x^2\right)}^9$                           c.    $f\left(x\right)=3{\sin }^3\frac{1}{x}+2{\cos }^2\frac{x}{2}$.
b.    $f\left(x\right)={\left(5+2x\right)}^3+\sqrt{2x+1}$
Jawab
a.    $f\left(x\right)={\left(2+3x^2\right)}^9$
      Misalkan,$u=2+3x^2$ maka $u^{\prime }\left(x\right)=6x$ sehingga $f\left(x\right)=u^9$
      $f^{\prime }\left(x\right)=9u^8·u^{\prime }\left(x\right)=9{\left(2+3x^2\right)}^8·6x=54x{\left(2+3x^2\right)}^8$
b.    $f\left(x\right)={\left(5+2x\right)}^3+\sqrt{2x+1}={\left(5+2x\right)}^3+{\left(2x+1\right)}^{\frac{1}{2}}$
      $f^{\prime }\left(x\right)=3{\left(5+2x\right)}^2·2+\frac{1}{2}{\left(2x+1\right)}^{-\frac{1}{2}}·2=6{\left(5+2x\right)}^2+\frac{1}{\sqrt{2x+1}}$
c.    $f^{\prime }\left(x\right)=3\left(3{\sin }^2\frac{1}{x}\right)\left(\cos \frac{1}{x}\right)\left(-\frac{1}{x^2}\right)+2\left(2\cos \frac{x}{2}\right)\left(-\sin \frac{x}{2}\right)\left(\frac{1}{2}\right)$
                $=-\frac{9}{x^2}{\sin }^2\frac{1}{x}\cos \frac{1}{x}-\sin \frac{x}{2}\cos \frac{x}{2}$